Обозначение единичного вектора | Векторы и пространства | Линейная алгебра | Ханская академия
Когда они объясняют размер W, он представлен как отрицательная сторона оси X. Почему размер W отрицателен X? Разве это не собственное измерение?

- Попробуйте нарисовать четырехмерный график на двухмерной поверхности. Это то, что они придумали (ваше право, хотя это не лучший график).
Как упоминал @NendoTaka, довольно сложно нарисовать 4d-объект на 2d-поверхности.
Вот как работает размерность:
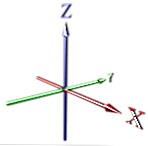
при одном измерении точка отправляется бесконечно, образуя линию (см. X)
в 2d мы добавляем размер, перпендикулярный этому (см. X, Y).
Затем мы снова идем перпендикулярно и расширяемся вверх, чтобы получить третье измерение (см. X, Y, Z).
Поскольку 3d> 2d, мы не можем хорошо представить это на бумаге, не сложив бумагу или не добавив на нее дополнительных листов - все это действительно непрактично для просмотра на экране. Поэтому вместо этого мы используем перспективу - то, как наши глаза воспринимают трехмерное изображение. Обычно углы здесь составляют ~ 30 градусов.

И это выглядит неплохо, потому что наши глаза не видят в этом традиционном трехмерном смысле, поэтому имитация работает. Но когда мы хотим представить 4-е измерение, нам не с чем его сравнивать. Нам нужно снова пойти перпендикулярно, и нашим глазам трудно это понять, так как у нас мало ориентира.
Вот пример изображения 4-го измерения:
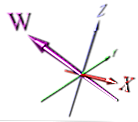
Это более правильный способ отображения измерения, но он по-прежнему опирается на перспективу - также на первый взгляд не сразу очевидно, что это новое измерение.
Вероятно, аниматоры предпочли сделать что-нибудь простое, что было бы легче анимировать. Хотя, если вы повернете изображение выше, размеры X и W могут перекрываться - и это не было бы очевидно на изображении без стрелок.
Так что да, они ошибаются - но также нет простого способа изобразить 4 измерения на одном листе бумаги.
Координаты источников изображений и хорошее чтение
3- 1 Честно говоря, существует множество стандартных способов проецирования 4-мерных объектов, таких как тессеракты и 3-сферы, в 3 измерения (а затем вниз до 2 измерений обычными способами), которые значительно превосходят тот, который используется в шоу, многие из которых имеют дополнительный бонус в виде более крутого вида, чем тот, который использовался в шоу.
- @senshin да, конечно, но я думаю, аниматоры тоже хотели что-то объяснить, а не поразить
- 1 Вы можете использовать другие вещи, кроме положения, чтобы указать, насколько далеко по оси что-то находится, например, цвет.